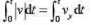求质点受力的情况。
如果结果不匹配，请 
更多“一质量为m的质点在xy平面上运动，其位矢为求质点受力的情况。”相关的问题
设一平面薄板(不计其厚度)，它在xy平面上的表示是由光滑的简单闭曲线围成的闭区域D。如果该薄板分布有面密度为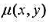
的电荷，且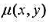在D上连续，试用二重积分表示该薄板上的全部电荷。
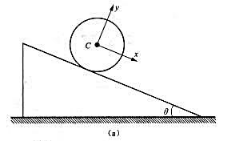
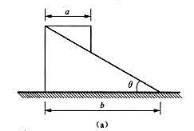
题10-18图(a)所示，一均质圆柱，质量为m,半径为r，无初速地放在倾角为θ的斜面上，轮与斜面的摩擦因数为f,若不计滚动阻力，试求其质心的加速度。
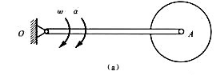
题11-5图(a)所示系统由均质圆盘与均质细杆铰接而成。已知圆盘半径为r，质量为M，质量为m。在图示水平位置杆的角速度为w，角加速度为a，圆盘的角速度，角加速度均为零，试求系统惯性力系向定轴O简化的主矢与主矩。
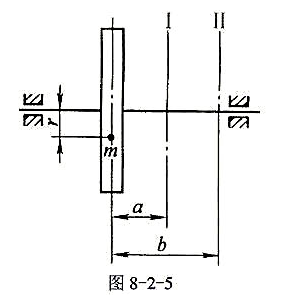
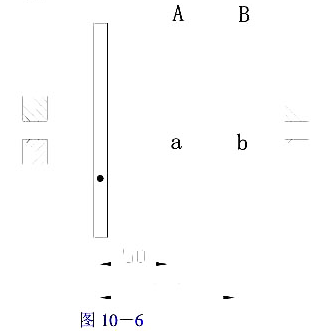
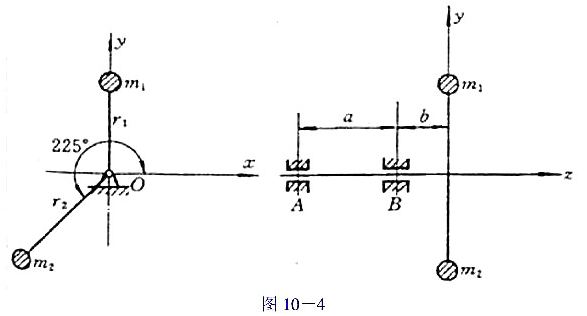
(1)因两集中质量的惯性力而在支承A、B处产生的动压力RA和RB的大小与方向;
(2)为使该回转件达到动平衡,在xOy平面上应加平衡质径积mbrb的大小和方向.
A.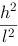
B.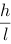
C.
D.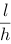
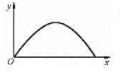
如图所示，质点在t=0时刻由原点出发作斜抛运动，其速度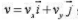
回到x轴的时刻为t，则
A.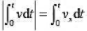
B.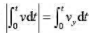
C.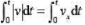
D.
