如果结果不匹配，请 
更多“假定I是一个唯一分解环而Q是I的商域。证明:I[x]的一个多…”相关的问题
1)设A为一个n级实矩阵，且|A|≠0，证明A可以分解成A=QT，其中Q是正交矩阵，T是上三角形矩阵：
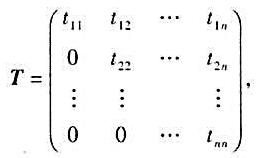
ii＞0(i=1，2，...，n)，并证明这个分解是唯一的;
2)设A是n级正定矩阵，证明存在一上三角形矩阵T，使A=T'T。
设f(α，β)是n维线性空间V上的非退化对称双线性函数，对V中一个元素α，定义V*中一个元素α*：α*(β)=f(α，β)，β∈V。
试证：1)V到V*的映射α→α*是一个同构映射;
2)对V的每组基ε1，...，εn，有V的唯一的一组基ε1'，...，εn'使f(εi，εj')=δij;
3)如果V是复数域上n维线性空间，则有一组基η1，...，ηn，使ηi=ηi'，i=1，...，n。
令V=Mn(C)是复数域上全体n阶矩阵所组成的n2维向量空间，令A是任意一个n阶复矩阵。如下地定义V的一个线性变换αA：V→V：对于任意X∈V=Mn(C)，αA(X)=AX-AX。
(i)证明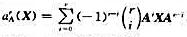
，r是非负整数，由此推出，如果A是幂零矩阵，那么αA是V的幂零变换;
(ii)如果A=D+N是A的若尔当分解，其中D是A的可对角化部分，N是幂零部分，那么αD和αN分别是线性变换αA的若尔当分解。
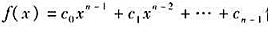使f(ai)=bi，i=1，2，...，n。
设A是一个n阶矩阵。并且存在一个正整数m使得Am=Q。
(i)证明I-A可逆，并且(I-A)-1=I+A+...+Am-1。
(i)求矩阵
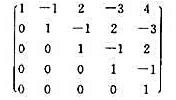
的逆矩阵。
设Fn={(x1，x2，...，xn)|xi∈F)是数域F上n维行空间。定义σ(x1，x2，...，xn)=(0，x1，...，xn-1)。
(i)证明：σ是Fn的一个线性变换，且σn=θ;
(i)求Ker(σ)和Im(σ)的维数。
A.i节点是一个长度固定的表
B.超级块在文件系统的个数是唯一的
C.i节点包含了描述一个文件所必需的全部信息
D.超级块记录了i节点表和空闲块表信息在磁盘中存放的位置
设A是复数域C上一个n阶矩阵，λ1，λ2，···，λn是A的全部特征根(重根按重数计算)。
(i)如果f(x)是C上任意一个次数大于零的多项式，那么f(λ1)，f(λ2)，···，f(λn)是f(A)的全部特征根;
(ii)如果A可逆，那么λi≠0，i=1，2，...，n，并且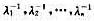
是A-1的全部特征根。
